A roller-coaster car might be represented by a block of mass 50.0kg. The automobile is released from rest at a height h = 51.0m over the floor and slides along a frictionless track. The car experiences a Loop of radius R = 17.0m at floor level, as revealed. As you will learn at the course of the Problem, the first elevation of 51.0m is excellent enough so the automobile never loses contact with this monitor.
1. Find an expression for the kinetic energy of the Automobile At the very peak of the loop.
2. Locate the minimal initial elevation hmin where the Vehicle Can be published which nonetheless allows the car to remain in touch Together with the track near the peak of the loop.
Solutions
1. K = mg(h – 2R) = 8330 J
2. hmin = 5R/2 = 42.5 m
If you Resolve the problem Together with variables Rather than Figures, you will Discover That the minimum height Needed is given by hmin=2.5R.
For h>2.5R the car can still finish the loop, needless to say. In cases like this, the standard power would be greater than zero at the peak of the loop.
For h<R the car would oscillate at the base region of the loop. Can you call this?
For R<h<2.5R, the car would eliminate contact with the trail before reaching the very top. That’s the reason why roller coasters need to have plenty of security features. If You Prefer, you should check the angle where the car gets contact with the monitor is given by θ=arcsin23(hR−1).
Interestingly, if you attempt to look at your lead to a college or a university laboratory with a metal or aluminum marble, then you will observe that the essential minimum height is higher than 2.5R. This is as a marble also offers rotational kinetic energy along with translational kinetic energy.
To find the kinetic energy in this case you can use the kinetic energy calculator.
Scroll the rest of the blog for more Q & A

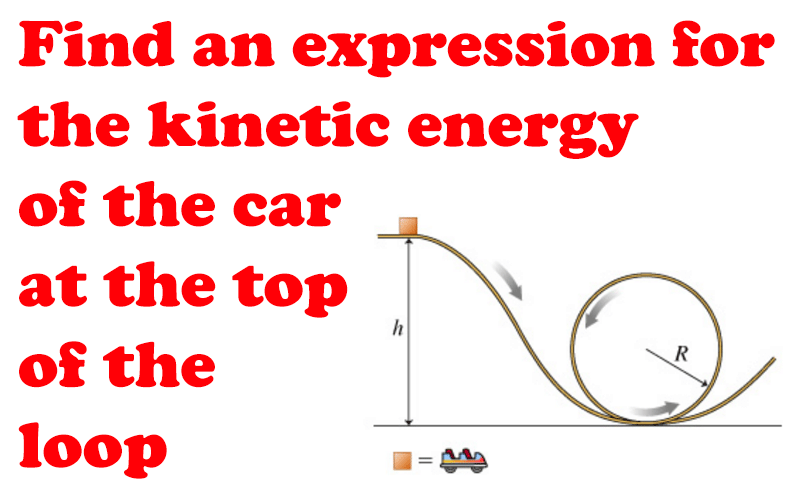
One thought on “Find an Expression for the Kinetic Energy of the Car at the Top of the Loop”